안녕하세요, 오늘은 고체역학에 필수적인 ‘Free-Body Diagram(FBD)’에 대해 알아보려고 합니다. Free-Body Diagram(FBD)는 강체나 변형 가능한 물체를 정적 분석하는 데 있어서 필수적인 요소입니다. 이 포스트를 통해 Free-Body Diagram(FBD)의 중요성과 그 작성 방법에 대해 이해하실 수 있을 것입니다.
Free-Body Diagram(FBD)는 물체에 작용하는 모든 힘을 나타내는 도표입니다. 이에는 적용된 힘과 모멘트, 반작용 힘과 모멘트, 개별 구성 요소 간의 연결 힘 등이 포함됩니다. 즉, 물체의 평형 상태를 정확히 이해하려면 이 모든 힘을 Free-Body Diagram(FBD)에 표시해야 합니다.
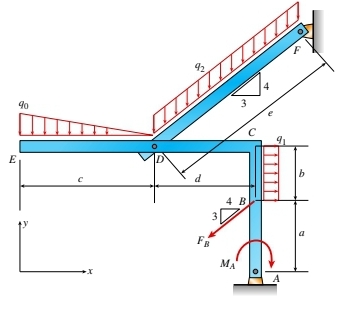
예를 들어, 아래의 그림 1에서 보이는 평면 프레임의 전체 Free-Body Diagram(FBD)는 그림 2(a)에 표시되어 있습니다. 이 Free-Body Diagram(FBD)에는 모든 적용 힘과 반작용 힘, 그리고 모든 분포하중에 대해 정적으로 동등한 집중 하중이 표시되어 있습니다. 분산된 하중 q0, q1, q2를 대표하기 위해 각각의 분산 하중의 중심에 작용하는 정적으로 동등한 힘 Fq0, Fq1, Fq2가 평형 방정식 해결에 사용됩니다.
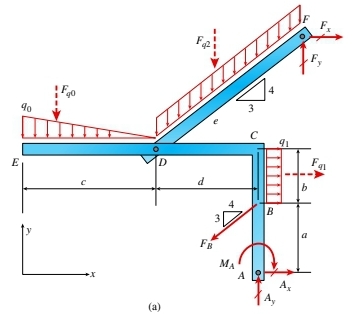
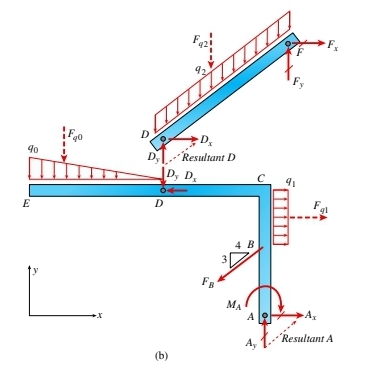
이어서, 그림 2(b)에서 보이는 것처럼 평면 프레임이 분해되어 각 프레임 부분에 대한 별도의 Free-Body Diagram(FBD)를 그릴 수 있습니다. 이렇게 하면 핀 연결 힘(Dx, Dy)이 드러나게 됩니다. 두 Free-Body Diagram(FBD)는 모두 핀 지지 결합 A에서의 반작용 힘 Ax와 Ay, 그리고 Fx와 Fy를 포함한 모든 적용 힘을 보여주어야 합니다.
이렇게 작성한 Free-Body Diagram(FBD)는 평형 상태를 판단하는데 중요한 역할을 합니다. 일반적으로, 지지 반응을 해결하기 위해 정적 기호 규칙이 사용되는데, 좌표 축의 양의 방향으로 작용하는 힘은 양수로 가정하고, 오른손 규칙을 사용하여 모멘트 벡터를 결정합니다.
Free-Body Diagram(FBD)는 물체에 작용하는 힘을 시각적으로 이해하고, 그 결과를 분석하는 데 도움이 되는 도구로 사용할 수 있습니다.
Free-Body Diagram(FBD)를 그리는 일반적인 과정
1. 먼저, 분석하고자 하는 물체를 선택합니다. 이 물체는 단일 물체일 수도 있고, 시스템의 일부일 수도 있습니다.
2. 선택한 물체를 주변 환경으로부터 ‘분리’합니다. 이는 물체에 작용하는 외부 힘만을 고려하기 위함입니다. 이 단계에서는 물체에 연결된 모든 외부 힘과 모멘트를 식별해야 합니다.
3. 물체에 작용하는 모든 힘을 식별합니다. 이에는 중력, 마찰력, 텐션 등이 포함될 수 있습니다. 또한, 작용점과 작용 방향도 명시해야 합니다.
4. 식별한 각 힘을 화살표로 표시합니다. 화살표의 길이는 힘의 크기를, 화살표의 방향은 힘의 방향을 나타냅니다. 힘의 작용점은 물체 위의 해당 위치에 화살표로 표시합니다.
5. 물체가 다른 물체나 표면에 의해 지지되거나 고정되어 있는 경우, 해당 지점에서 반작용 힘을 고려해야 합니다. 이 힘은 물체를 지지하거나 고정하는 데 필요한 힘으로, 일반적으로 지지점에서 물체로 향하는 방향을 가집니다.
6. (모든 힘을 화살표로 표시한 후, 각 힘을 물리적 현상을 나타내는 적절한 심볼로 마지막니다. 예를 들어, 중력은 ‘W’ 또는 ‘mg’, 마찰력은 ‘f’, 텐션은 ‘T' 등으로 표시할 수 있습니다.)
7. 마지막으로, 모든 힘의 벡터 합을 계산합니다. 이 힘의 합이 0이면 물체는 정적 상태에 있습니다.
여기까지 FBD에 대한 설명이였습니다. 감사합니다.
출처: [1] Mechanics of materials, JM Gere, BJ Goodno et. al - 2012 - Cengage learning
'역학 > 고체역학(재료역학)' 카테고리의 다른 글
| 재료역학: 기존 응력의 사용 제한 조건 알아보기 (0) | 2023.12.08 |
|---|---|
| 재료 역학: 응력(stress[스트레스])이란? (1) | 2023.12.07 |
| 기계공학과: 4대 역학: 고체역학(재료역학) (1) | 2023.11.29 |
| 탄성 구간 해석: 후크의 법칙(Hook's law) (3) | 2023.11.20 |
| 응력-변형률 곡선(Stress-Strain curve[SS curve])의 이해 (1) | 2023.11.17 |